7.6 Movimientos a través del árbol  

No hay mucho que contar. Nuestra estructura se referenciará siempre mediante un puntero al nodo Raiz, este puntero no debe perderse nunca.

Para movernos a través del árbol usaremos punteros auxiliares, de modo que desde cualquier puntero los movimientos posibles serán: moverse al nodo raíz de la rama izquierda, moverse al nodo raíz de la rama derecha o moverse al nodo Raiz del árbol.

7.7 Información  

Hay varios parámetros que podemos calcular o medir dentro de un árbol. Algunos de ellos nos darán idea de lo eficientemente que está organizado o el modo en que funciona.

Comprobar si un árbol está vacío.

Un árbol está vacío si su raíz es NULL.

Calcular el número de nodos.

Tenemos dos opciones para hacer esto, una es llevar siempre la cuenta de nodos en el árbol al mismo tiempo que se añaden o eliminan elementos. La otra es, sencillamente, contarlos.

Para contar los nodos podemos recurrir a cualquiera de los tres modos de recorrer el árbol: inorden, preorden o postorden, como acción sencillamente incrementamos el contador.

Comprobar si el nodo es hoja.

Esto es muy sencillo, basta con comprobar si tanto el árbol izquierdo como el derecho están vacíos. Si ambos lo están, se trata de un nodo hoja.

Calcular la altura de un nodo.

No hay un modo directo de hacer esto, ya que no nos es posible recorrer el árbol en la dirección de la raíz. De modo que tendremos que recurrir a otra técnica para calcular la altura.

Lo que haremos es buscar el elemento del nodo de que queremos averiguar la altura. Cada vez que avancemos un nodo incrementamos la variable que contendrá la altura del nodo.

• Empezamos con el nodo raíz apuntando a Raiz, y la 'Altura' igual a cero.
• Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos la búsqueda y el valor de la altura es 'Altura'.
• Incrementamos 'Altura'.
• Si el valor del nodo raíz es mayor que el elemento que buscamos, continuaremos la búsqueda en el árbol izquierdo.
• Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos la búsqueda en el árbol derecho.

Calcular la altura de un árbol.

La altura del árbol es la altura del nodo de mayor altura. Para buscar este valor tendremos que recorrer todo el árbol, de nuevo es indiferente el tipo de recorrido que hagamos, cada vez que cambiemos de nivel incrementamos la variable que contiene la altura del nodo actual, cuando lleguemos a un nodo hoja compararemos su altura con la variable que contiene la altura del árbol si es mayor, actualizamos la altura del árbol.

• Iniciamos un recorrido del árbol en postorden, con la variable de altura igual a cero.
• Cada vez que empecemos a recorrer una nueva rama, incrementamos la altura para ese nodo.
• Después de procesar las dos ramas, verificamos si la altura del nodo es mayor que la variable que almacena la altura actual del árbol, si es así, actualizamos esa variable.

7.8 árboles degenerados  

Los árboles binarios de búsqueda tienen un gran inconveniente. Por ejemplo, supongamos que creamos un ABB a partir de una lista de valores ordenada:

2, 4, 5, 8, 9, 12

Difícilmente podremos llamar a la estructura resultante un árbol:

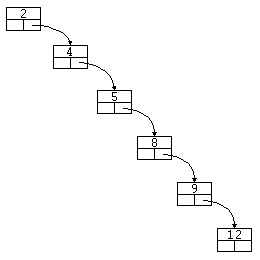
Esto es lo que llamamos un árbol binario de búsqueda degenerado, y en el siguiente capítulo veremos una nueva estructura, el árbol AVL, que resuelve este problema, generando árboles de búsqueda equilibrados.